|
|
EXERCICE 1
(4 points)
Commun à tous les candidats
PROBABILITES
|
I- Lors de la préparation d'un concours, un éléve n'a étudié
que 50 des 100 leçons. On a mis 100 papiers contenant chacun une
question dans une urne, ces questions portant sur des leçons différentes.
Le candidat tire simultanément au hasard 2 papiers.
On donnera les réponses sous forme de fractions irréductibles.
- Quelle est la probabilité qu'il ne connaisse
aucun de ces sujets ?
- Quelle est la probabilité qu'il connaisse les
deux sujets ?
- Quelle est la probabilité qu'il connaisse un et
un seul de ces sujets ?
- Quelle est la probabilité qu'il connaisse au
moins un de ces sujets ?
II- On considère maintenant que l'élève a étudié n des
100 leçons. ( n étant un entier inférieur ou égal à 100).
- Quelle est la probabilité pn qu'il
connaisse au moins un de ces sujets ?
- Déterminer les entiers n tels que pn
soit supérieur ou égal à 0,95.
|
EXERCICE 2
(5 points)
Candidats ayant suivi l'enseignement de spécialité
|
Les trois parties I, II, III peuvent être traitées indépendamment
les unes des autres.
I - Soit E = 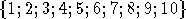 .
.
Déterminer les paires 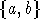 d'entiers distincts de E tels que le reste de la division euclidienne
de ab par 11 soit 1.
d'entiers distincts de E tels que le reste de la division euclidienne
de ab par 11 soit 1.
II-
- Soit n un entier naturel supérieur ou égal à
3.
- L'entier
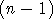 !
+ 1 est-il pair ? !
+ 1 est-il pair ?
- L'entier
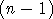 !
+ 1 est-il divisible par un entier naturel pair ? !
+ 1 est-il divisible par un entier naturel pair ?
- Prouver que l'entier
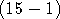 !
+ 1 n'est pas divisible par 15. !
+ 1 n'est pas divisible par 15.
- L'entier
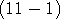 !
+ 1 est-il divisible par 11 ? !
+ 1 est-il divisible par 11 ?
III- Soit p entier naturel non premier (p  2).
2).
- Prouver que p admet un diviseur q (1 <
q < p) qui divise
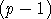 !. !.
- L'entier q divise-t-il l'entier :
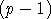 !
+ 1 ? !
+ 1 ?
- L'entier p divise-t-il l'entier :
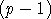 !
+ 1 ? !
+ 1 ?
|
EXERCICE 2
(5 points)
Candidats n'ayant pas suivi l'enseignement de spécialité
|
Le plan orienté est rapporté au repère orthonormal 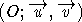 ,
l'unité graphique étant 4 cm. ,
l'unité graphique étant 4 cm.
On considère les points A0, A1 d'affixes
respectives :
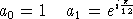
Le point A2 est l'image du point A1 par la
rotation r de centre O et d'angle 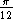 . .
On considère la fonction numérique f définie sur ![]- oo , 1[](annales/b118x.gif) par :
par :
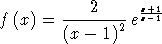
On désigne par  la courbe représentative de f dans le plan rapporté à un repère
orthonormal
la courbe représentative de f dans le plan rapporté à un repère
orthonormal  , l'unité graphique étant 2 cm.
, l'unité graphique étant 2 cm.
I-
- Etudier les variations de f.
- Tracer la courbe
 . .
II-
- Déterminer une primitive de f sur
![]- oo , 1[](annales/b127x.gif) .
.
- Soit
 réel tel que 0 <
réel tel que 0 <  < 1, déterminer :
< 1, déterminer :
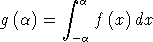
- Quelle est la limite de g
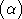 quand
quand  tend vers 1.
tend vers 1.
- Quelle est l'aire en cm2 du domaine
limité par la courbe de f, l'axe des abscisses, les droites d'équations
respectives x = -
 et x =
et x =  . .
III-
- Soit a un élément de
![]- oo , 1[](annales/b132x.gif) . Déterminer graphiquement, en fonction de a, le nombre de
solutions de l'équation f
. Déterminer graphiquement, en fonction de a, le nombre de
solutions de l'équation f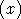 = f
= f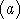 .
.
|