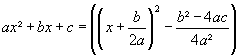
MATHÉMATIQUES
Second degré et polynômes
1. Second degré.
A. Factorisation du trinôme de forme ax² + bx +c.
- Un trinôme du second degré est une fonction de la forme x ® ax² + bx + c ,
où a, b, c sont des réels, avec a ¹ 0.
- Forme canonique du trinôme :
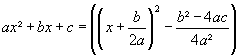
- Soit l'équation ax² + bx + c = 0 , on pose D = b²- 4ac , où D est le
discriminant du trinôme.
* D < 0 : pas de solution.
* D = 0 : une solution unique :
![]()
* D > 0 : deux solutions :
![]()
- Factorisation du trinôme :
* D < 0 : pas de factorisation.
* D = 0 :
![]()
* D > 0 :
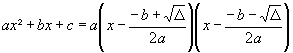
B. Somme et produit des racines.
Lorsque le trinôme ax² + bx + c admet deux racines distinctes ou confondues,
leur somme S et leur produit P sont donnés par :
![]()
Deux réels ont pour somme S et pour produit P si et seulement s'ils sont solutions
de l'équation x²- Sx + P = 0.
C. Signe du trinôme.
Si D > 0, le trinôme ax² + bx + c est du signe de a à l'extérieur de racines, et du
signe de -a entre les racines.
Si D £ 0, le trinôme ax² + bx + c est du signe de a pour tout x réel.
D. Variations du trinôme.
Soit le trinôme ax² + bx + c.
Si a > 0 , le trinôme admet un minimum en -b/2a.
Si a < 0 , le trinôme admet un maximum en -b/2a.
2. Polynômes.
A. Définition.
On appelle fonction polynôme toute fonction de la forme :
x ® P(x) = anxn+an-1xn-1+...+a1x+a0
n est le degré du polynôme.
B. Propriétés.
- Si la fonction x ® anxn+an-1xn-1+...+a1x+a0 est la fonction nulle, alors :
an = an-1 = ... = a1 = a0 = 0.
- Soit f un polynôme non nul. f admet alors une écriture unique de la forme
x ® anxn+an-1xn-1+...+a1x+a0 avec a0 ¹ 0.
- Un polynôme est nul si et seulement si tous ses coefficients sont nuls.
Deux polynômes non nuls sont égaux si et seulement si :
* ils ont même degré.
* les coefficients des termes de même degré sont égaux.
- Le produit de deux polynômes non nuls est un polynôme ayant pour degré la
somme des degré des polynômes.
C. Factorisation.
- On appelle racine d'un polynôme P tout réel x0 tel que P(x0) = 0.
- On dit qu'un polynôme P est factorisable par x - a s'il existe un polynôme Q
tel que P(x) = (x-a) Q(x).
- Pour tout polynôme P, le polynôme P(x)-P(a) est factorisable par x-a.
- Le polynôme P est factorisable par x-a si et seulement si P(a) = 0.
- Méthodes pour la factorisation :
* la division euclidienne.
* l'identification.
* la factorisation de P(x)-P(a).