On dit que f est dérivable en x0 si et seulement
si le taux d’accroissement ![]()
admet une limite finie A lorsque h tend vers 0.
-
f
est dérivable en x0 si et seulement s’il
existe :
MATHÉMATIQUES
Dérivation
1. Définition.
On dit que f est dérivable en x0 si et seulement
si le taux d’accroissement ![]()
admet une limite finie A lorsque h tend vers 0.
f
un réel A
une fonction
telle que
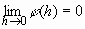
tels que : ![]()
Le nombre A est appelé nombre dérivé de f en x0, noté f’(x0).
L’application affine h g f(x0)+Ah est appelé fonction affine tangente à f au point x0.
Cas de non - dérivabilité : si le taux d’accroissement n’a pas de limite, a une limite infinie ou une limite différente à gauche et à droite.
2. Dérivées.
u et v sont deux fonctions.
|
f |
f’ |
|
b |
0 |
|
ax+b |
a |
|
x² |
2x |
|
x3 |
3x² |
|
xn |
nxn-1 |
|
|
|
|
|
|
|
u+ v |
u’ + v’ |
|
ku |
kv |
|
uv |
u’v + uv’ |
|
|
|
|
un |
nu’ un-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
f (ax+b) |
af’ (ax+b) |
|
sin x |
cos x |
|
cos x |
- sin x |
|
tan x |
1 + tan² x
|
|
sin (ax+b) |
a cos(ax+b) |
|
cos (ax+b) |
- a sin(ax+b) |
3. Applications à la dérivation.
A. Variations d’une fonction.
Soit f une fonction dérivable sur un intervalle I .
Si f’ est strictement positive (peut-être nulle en des points isolés), alors f est strictement croissante sur I .
Si f’ est strictement négative (peut-être nulle en des points isolés), alors f est strictement décroissante sur I.
Si f’ est nulle sur I , alors f est croissante sur I .
Soit f une fonction dérivable sur un intervalle ouvert I et x0 un réel élément de I .
Si la dérivée f’ s’annule en x0 en changeant de signe, alors f(x0) est un extremum local de f sur I.
B. Tangente à une courbe.
Équation d’une tangente (T) en x0 à la courbe :
![]()
C. Vitesse moyenne et vitesse instantanée.
Vitesse moyenne entre t1 et t2 :
![]()
Vitesse instantanée en t1 : ![]()
D. Bijection.
Soit f une fonction dérivable et strictement monotone sur un intervalle [a ; b]. Alors f
est une bijection de [a ; b] sur : [f(a) ; f(b)] si f est strictement croissante.
[f(b) ; f(a)] si f est strictement décroissante.
L’équation
,
[f(a) ; f(b)] ou [f(b) ; f(a)] , admet alors une solution et une
seule. En particulier, si f(a).f(b) < 0 , l’équation f(x) = 0 admet une solution unique
dans [a ; b].