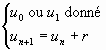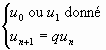MATHÉMATIQUES
Suites
1. Généralités.
A. Définition.
Toute fonction de N dans R, définie
à partir d’un certain rang, est appelée suite numérique.
On peut définir des suites de deux manières :
-
Formule explicite : de la forme
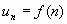 où
où 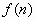 est
une fonction de R dans R. Ex :
est
une fonction de R dans R. Ex : 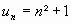
-
Formule de récurrence : elle
est définie par la donnée d’un procédé de calcul permettant d’exprimer
un terme à l’aide du précédent (formule de récurrence) et par une
condition initiale qui fixe la valeur du premier terme.
Ex : 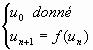 avec
avec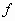 fonction de R dans R.
fonction de R dans R.
B. Suites croissantes
et décroissantes, suites majorées, minorées
et
bornées.
Pour étudier la monotonie de 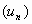 , on peut utiliser deux
techniques :
, on peut utiliser deux
techniques :
-
La différence 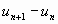 .
.
-
Le quotient 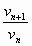 si
si
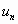 > 0 .
> 0 .
entier n : 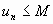 .
.
Une suite 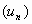 est dite minorée, lorsqu’il existe un
réel m tel que, pour
est dite minorée, lorsqu’il existe un
réel m tel que, pour
tout entier n : 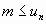 .
.
Une suite à la fois majorée et minorée est dite bornée.
2. Suites arithmétiques.
A. Définition.
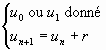
avec r
raison de la suite arithmétique.
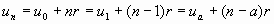
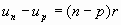
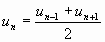
B. Somme des n premiers termes.

Ex : 1 + 2 + 3 + 4 + 5 + 6 + ….+ 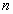 =
=
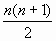
3. Suites géométriques.
A. Définition.
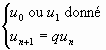
avec q
raison de la suite arithmétique.
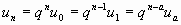
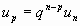
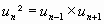
B. Somme des n premiers termes.
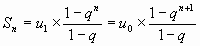

4. Limites de suites numériques.
5. Raisonnement par récurrence.
Démontrer une propriété P qui dépend d’un
entier naturel n.
-
Etablir ou vérifier que P est vraie
pour 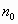 .
.
-
Supposer que pour 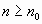 ,
P(n) est vraie (HYPOTHESE DE RECURRENCE)
,
P(n) est vraie (HYPOTHESE DE RECURRENCE)
-
Démontrer alors que P(n+1) est
vraie.
6. Savoir-faire.
Ramener l’étude d’une suite
quelconque à celle d’une suite géométrique en substituant par une autre
variable.
Retrouver graphiquement les termes d’une
suite.
Retour
au Menu Fiches Maths Première
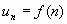 où
où 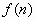 est
une fonction de R dans R. Ex :
est
une fonction de R dans R. Ex : 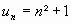
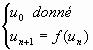 avec
avec