MATHÉMATIQUES
Probabilités
1. Vocabulaire.
-
Une expérience aléatoire est
une expérience dont le résultat (issue) dépend du hasard.
On en connaît le protocole expérimental (conditions
expérimentales), et l’ensemble des résultats possibles ou éventualités,
c’est-à-dire l’univers.
-
On appelle événement toute
partie de l’univers des possibles.
-
Exemples : lancement d’un dé
cubique numéroté de 1 à 6. Quelle est la probabilité d’obtenir un …
sur la face supérieure ?
|
Vocabulaire des
Probabilités |
Vocabulaire des
Ensembles |
Exemples |
|
Univers |
Ensemble |
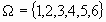
|
|
Eventualité |
Elément |
5 |
|
Evénement
élémentaire |
Singleton |
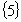
|
|
Evénement |
Partie ou
sous-ensemble |
A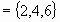 |
|
Evénement certain |
Partie pleine |
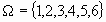
|
|
Evénement impossible |
Partie vide |
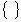
|
|
Evénement
" A et B " |
Intersection de deux
parties |
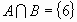 avec B : obtenir un multiple de 3.
avec B : obtenir un multiple de 3.
|
|
Evénement
" A ou B " |
Réunion de deux
parties |
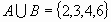
|
|
Evénements
incompatibles |
Parties disjointes |
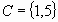 
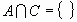
|
|
Evénements
contraires |
Parties
complémentaires |
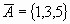
|
2.
Lois de probabilités et propriétés.
A. Définition.
L’ensemble des parties d’un ensemble
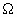 est noté
est noté 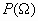 .
.
On appelle probabilité toute
application 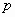 :
: 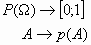
Et qui vérifie : 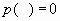
Si A et B sont incompatibles, c’est-à-dire
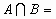 , alors :
, alors :
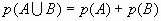
B. Propriétés.
C. Équiprobabilité.
Lorsque toutes les issues ont la même
probabilité, on dit qu’il y a équiprobabilité. Dans ce cas, si l’univers
des issues 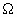 a N éléments, quelle que soit l’issue
a N éléments, quelle que soit l’issue 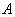 ,
,
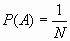 . On a donc :
. On a donc : 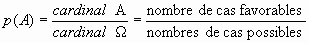 .
.
3. Dénombrement.
Retour
au Menu Fiches Maths Première
![]()
![]()
![]()
![]()
![]()
![]() avec B : obtenir un multiple de 3.
avec B : obtenir un multiple de 3.![]()
![]()
![]()
![]()
![]()