MATHÉMATIQUES
Produit Scalaire
1. Définition.
Étant donné deux vecteurs non nuls ![]() et
et
![]() , on appelle produit scalaire de
, on appelle produit scalaire de ![]() et
et
![]() , noté
, noté ![]() , le réel
, le réel ![]() où :
où :
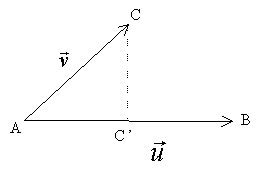
2. Propriétés.
![]()
![]()
![]() et
et ![]()
![]()
![]()
![]()
![]() et
et ![]() sont perpendiculaires si
sont perpendiculaires si ![]() et
et ![]() différents de 0.
différents de 0.
![]()
![]()
3. Expression analytique du produit scalaire.
![]() avec
avec ![]() et
et ![]()
(![]() ^
^![]() )
)
![]()
![]() et si
et si ![]() ,
, ![]()
Tangente à un cercle de centre C(a,b) en A(xa,ya) :
(xa-a)( x-xa)+(ya-b)( y-ya) = 0
Équation cartésienne d’un cercle :
défini par son centre C(a,b) et un point A(xa,xb) :
(x-a)²+(y-b)² = R² = (xb-a)²+(ya-b)²
défini par un diamètre [AB] : (x-xa)( x-xb)+(y-ya)( y-yb) = 0
4. Relations métriques
dans le triangle.
A. Théorème d’Al Kashi.
Dans un triangle de côté a, b, c et d’angle A, B, C, on a :
a
b
c
B. Théorème de la médiane.
Dans un triangle AMB, avec O centre de [AB] :
MA
MA
![]()
C. Lignes de niveau.
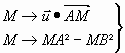 Droites
orthogonales à
Droites
orthogonales à ![]() ou
ou ![]() .
.
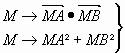 Cercles centrés
au milieu de [AB].
Cercles centrés
au milieu de [AB].