A. Actions mécaniques.

• Effets : mettre un objet en mouvement, modifier la trajectoire, arrêter l’objet, modifier sa vitesse, déformer un objet…

• Forces de contact : musculaire, pressante, frottement, élastique.

• Forces à distance : gravitation, électrique, magnétique.

• Forces localisée / répartie.

       B. Vecteur force.

Caractéristiques :

• direction

• sens

• origine

• intensité / norme : en Newton (N)

Si un objet est soumis à deux forces appliquées en un même point, cette action peut-être représentée par une force unique qui est la somme des deux forces.

       C. Principe d’interaction.

Lorsqu’un corps A exerce sur un corps B une force notée F_{A ®B}, le corps B exerce sur A au même moment une force F_{B ®A} telle que :

F_{A ®B} = - F_{A ®B} et F_{A ®B} + F_{A ®B} = 0

C’est la force d’attraction de la Terre sur un corps.

• Direction : verticale

• Sens : de haut en bas

• Norme : intensité : P(poids en N) = m(masse en kg) ´ g(intensité de la pesanteur en N.kg^-1)

• Point d’application : on peut considérer que le poids est localisé au centre d’inertie.

La poussée d’Archimède résulte des forces pressantes exercées par les fluides (gaz et liquides) sur les surfaces des solides immergées.

• Direction : verticale

• Sens : de bas en haut

• Point d’application : centre de gravité du liquide déplacé

• Norme : intensité , égale au poids du liquide déplacé.

• Tension d’un fil : la tension T d’un fil tendu de masse négligeable est la valeur des forces que le fil exerce sur des objets liés à ses extrémités.

• Tension d’un ressort : de même, la tension T d’un ressort est exprimé par la formule :  , différence de longueur du ressort en m, et k constante de raideur du ressort en N.m^-1 .

      D. Réaction d’un plan sur un solide.

• Pas de frottements : la réaction est normale au plan.

• Avec frottements : la réaction n’est pas perpendiculaire au plan, et peut-être décomposée : les deux composantes s’appellent réaction normale et réaction tangentielle . On a donc : .

  La composante tangentielle s’appelle force de frottement, et s’oppose aux glissements du plan.

• Système isolé – système pseudo isolé :

• Un système mécaniquement isolé est un système qui n’est soumis à aucune force.

• Un système pseudo isolé est un système soumis à des forces dont la somme est nulle.

• Principe d’inertie :

• Dans un référentiel galiléen, le vecteur vitesse du centre d’inertie d’un solide isolé ou pseudo isolé est un vecteur constant. 

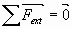
= constant

• Inversement, si dans un référentiel galiléen , le vecteur du centre d’inertie d’un solide est constant, alors le solide est pseudo isolé, et la somme des forces qui lui sont appliquées est nulle.

= constant

• Pour un solide en équilibre soumis à deux forces et  :

• Pour un solide en équilibre soumis à trois forces , et  : . De plus, les trois forces sont coplanaires et concourantes.

      C. Cas où

• Lois de la chute libre :

• Lorsque , on vérifie que et ont même direction et même sens. Dans un référentiel considéré comme galiléen, c’est donc la somme des forces extérieures agissant sur le système qui détermine le mouvement du centre d’inertie G.

   4.   Rotation d’un solide – Couple.

       A. Solide soumis à deux forces de somme nulle.

• Deux forces de même support, de somme vectorielle nulle, ne modifient pas l’équilibre d’un solide, ni son mouvement.

• Deux forces de somme vectorielle nulle et de supports différents constituent un couple qui peut provoquer la rotation du corps sur lequel il est appliqué. L’efficacité d’un couple dépend de l’intensité commune aux deux forces, et de la distance entre les supports des deux forces.

• Définition : la valeur absolue du moment M d’un couple de forces orthogonales à l’axe de rotation (D) est égale au produit de l’intensité des deux forces par la distance entre leur droite d’action : avec M en N.m, F en N et d en m.

• Le signe du moment dépend du sens de rotation choisi.

• Couple résistant / moteur :

• Un couple de forces est moteur si son action tend à faire tourner le solide dans le sens de rotation.

• Un couple de forces est résistant si son action tend à faire tourner le solide dans le sens inverse de rotation.

• Exercer la force sur un solide revient à exercer un couple de forces dont la deuxième force est appliquée sur l’axe de rotation.

• Le moment d’une force située dans un plan perpendiculaire à l’axe de rotation d’un solide, par rapport à cet axe, est égal au produit de la distance r du support de la force à l’axe, appelé bras de levier, avec la norme F de la force :

• Un solide mobile autour d'un axe de rotation fixe est en équilibre ou en mouvement de rotation uniforme si la somme algébrique des moments des couples auxquels il est soumis est nulle :

• Inversement :

• Si , la vitesse de rotation n’est pas constante.

• Couple de torsion :

avec :

M moment en N.m

C constante de torsion en N.m.rad^-1

a angle de torsion en rad

• Puissance du couple moteur :

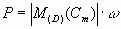
avec :

M moment en N.m

P puissance en W

w vitesse angulaire en rad.s^-1

 

 

Retour au Menu Fiches Physique - Chimie Première