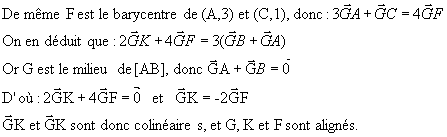DEVOIR MATHÉMATIQUES

N°2

Exercice 1 (5 points)

1) 4x² - 20x + 25 = 0 équivaut à (2x + 5)² = 0   

    D'où : x = 5/2

2)

    Le trinôme admet donc 2 racines distinctes.

     Donc le trinôme n'admet pas de racine et est du signe de a = -5/4 pour tout x réel.

     Donc le trinôme est négatif pour tout x réel.

     Il n'y a donc pas de solution dans R à cette inéquation.

     Après simplifications de l'inéquation on obtient :

     D'où étude de -7x² + 45x - 50 :

     Après construction du tableau de signes, on en déduit que (1 et 2 étant exclus) :

Exercice 2 (3,5 points)

1)

   Donc est racine de ce trinôme.

   Le produit des racines est :

   D'où l'autre racine : 

2) Soient x et y les dimensions du rectangle. On a xy = 120 et x² + y² = 17² = 289

    Or (x + y)² = (x² + y²) + 2xy , d'où (x + y)² = 289+2*120 = 529

    On en déduit que x + y = 23. Le demi-périmètre est égal à 23 cm.

    x et y sont les solutions de l'équation X² - 23X + 120 = 0

    Après résolution de cette équation, on trouve les dimensions du rectangle : 8 cm et 15 cm.

Exercice 3 (2,5 points)

Le triangle BCK est rectangle isocèle, donc KB = KC = d.

L'aire du trapèze est : 

D'où : 3d² + 42d = 360 et finalement d² + 14d - 120 = 0.

Après résolution de l'équation, on trouve une solution négative, d = -20, qui est à rejeter, et une solution positive et finale qui est d = 6.

Exercice 4 (4 points)

1) Pour la construction, on a : 

2) D'après la propriété fondamentale du barycentre : 

    Donc MI = MJ, et l'ensemble des points M est la médiatrice du segment IJ.

     L'ensemble des points M est le cercle de centre J et de rayon 0,5 AB.

Exercice 5 (5 points)

1) I est le barycentre de (A,3), (B,3) et (C,1).

    Donc, d'après le théorème du barycentre partiel, I est le barycentre de (A,3) et (E,4).

    D'où : A, E et I sont alignés.

2) On sait que I appartient à (AE). De la même manière que dans la première question, on peut démontrer que I est le barycentre de (B,3) et (F,4), donc I appartient à (BF). De plus I est le barycentre de (C,1) et (G,6) : I appartient donc à (GC).

Les trois droites (AE), (BF), et (GC) sont donc concourantes en I.

3) K est le barycentre de (B,3) et (C,-1).