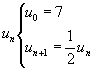|
Exercice 1 (4 points) Soit (un) la distance séparant deux ricochets après le nième ricochet, et Dn la distance totale parcourue par le caillou. On a : Dn = u0 + u1 +u2+ u3+ u4 +... +un (un) est une suite géométrique telle que :
La somme des n premiers termes est : Dn = 14 ´ [1-0,5n+1] D'où : la distance maximale parcourue par la pierre est la limite de Dn, soit 14m. La pierre n'arrive pas à l'autre berge.
Exercice 2 (8 points) 1) Soit (un) la distance pour aller au nième arbre. (un) est une suite arithmétique de 1er terme u1 = 0 et de raison r = 2. La distance parcourue par Colas sera : Dn = (u1 +u2+ u3+ u4 +... +u100) ´ 2 D'où : Dn = 19800 m, ainsi l'instituteur a raison... et pour faire l'aller-retour Arzano. 2) Soit (un) la distance pour aller au nième arbre, en partant de la fontaine. La distance totale parcourue par Arsène sera : Dn = 2 ´ (u1 +u2+ u3+ u4 +... +un) (un) est une suite arithmétique de 1er terme u1 = 20 et de raison r = 5. un = 5n + 15 La distance totale sera donc : Dn = 2n (5n + 35) = 5550 D'où, après résolution de l'équation : n = 30 arbres.
Exercice 3 (8 points) Non corrigé. |