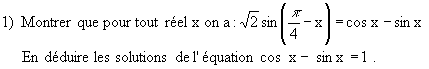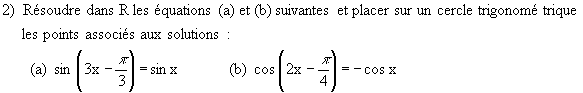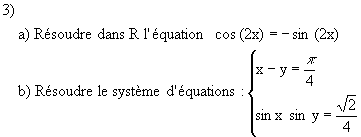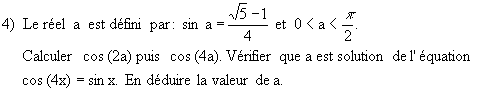|
Exercice 1 Dans cet exercice les questions 1 , 2 , 3 et 4 sont indépendantes.
Exercice 2
Problème
Partie A ABCD est un parallélogramme de centre O. Les points I et K sont tel que :
Les droites (BK) et (DI) coupent (AC) respectivement en J et L. 1) Montrer qu'il existe deux réels x et y tels que I est le barycentre de (A,x) et (B,y) et K est le barycentre de (C,x) et (D,y).
Partie B Dans cette partie ABCD est un carré, tel que AB = 15. On définit les points I, J, K et L comme dans la partie A dont on pourra utiliser les résultats.
Partie C Dans cette partie, on aborde la même figure que dans la partie B par une méthode analytique et on utilisera aucun des résultats trouvés dans la partie B.
|